Universidad Nacional Autónoma de México
Facultad de Estudios Superiores Acatlán
Matemáticas Aplicadas y Computación
Docente: Sergio Alejandro Matías Hernández
Manuel de Jesús Reyes Rubio
Estadística I
10/10/2010
Índice
I. Introducción Distribuciones Binomial, Poisson, Normal
I.I. Distribución Binomial
a.Función de probabilidad
b.Función generadora de momentos
c.Función característica
d.Ejemplo
I.I.l. Distribución Poisson
a.Función de distribución
b.Función generadora de momentos
c.Función de distribución(cdf) d.Función característica
I.V. Distribución Normal
a.función de densidad
b.función de distribución
c.función generadora de momentos
d.función característica
e.Ejemplo
V. Complemento
a. El Teorema del Límite Central
Introducción Distribuciones Binomial, Poisson, Normal
En este trabajo estudiaremos dos de las principales distribuciones de variables aleatorias discretas y la distribución Normal que se puede aplicar tanto para variables aleatorias discretas como para variables aleatorias continuas.
Una distribución de probabilidades para una variable aleatoria discreta es un listado mutuamente excluyente de todos los resultados numéricos posibles para esa variable aleatoria tal que una probabilidad específica de ocurrencia se asocia con cada resultado.
El valor esperado de una variable aleatoria discreta es un promedio ponderado de todos los posibles resultados, donde las ponderaciones son las probabilidades asociadas con cada uno de los resultados.
Distribución Binomial
Para hablar de la distribución Binomial primero tenemos que decir que esta dada por la sumatoria de eventos bernoulli, la distribución de Bernoulli (o distribución dicotómica), nombrada así por el matemático y científico suizo Jakob Bernoulli, es una distribución de probabilidad discreta, que toma valor 1 para la probabilidad de éxito (p) y valor 0 para la probabilidad de fracaso (q = 1 − p).
Si X es una variable aleatoria que mide "número de éxitos", y se realiza un único experimento con dos posibles resultados (éxito o fracaso), se dice que la variable aleatoria X se distribuye como una Bernoulli de parámetro p.
X˜Be(p)
La fórmula será:
f(x) = px(1 − p)1 − x con x = {0,1}
Su función de probabilidad viene definida por:

La distribución binomial es una distribución de probabilidades que surge al cumplirse cinco condiciones:
En cada ensayo hay sólo dos posibles resultados,
En cada ensayo, los dos resultados posibles son mutuamente excluyentes,
Los resultados de cada ensayo son independientes entre si, y
La probabilidad de cada resultado posible en cualquier ensayo es la misma de un ensayo a otro.
Su función de probabilidad es
La esperanza y la varianza son
La Función de Distribución de la v.a. Binomial
Las siguientes características son las que describen a una distribución Binomial
Función generadora de momentos (mgf)
Función característica
Ejemplo:
Supóngase que en cierta población el 52 por ciento de todos los nacimientos que se registraron son varones. Si aleatoriamente se escogen cinco registros de nacimientos dentro de esa población, ¿cuál es la probabilidad de que exactamente tres de ellos pertenezcan a varones?
Tenemos los siguientes datos:
N = 5 X = 3 p = 0.52
A continuación se muestra como resolverlo en Excel
En la categoría escogemos distr.binom y colocar los datos como se muestra
En la pantalla se mostrara el resultado es =0.323960832.
A continuación se anexa la pantalla de cómo se resuelve en R.
Distribución Poisson
La distribución Poisson fue nombrada así en honor a Denise Poisson en su libro Recherchés sur la probabilité des jugements...., un trabajo importante en probabilidad publicado en el año 1837, la distribución de Poisson recién aparecía. La distribución de Poisson describe la probabilidad como un acontecimiento fortuito ocurrido en un tiempo o intervalo de espacio bajo las condiciones que la probabilidad de un acontecimiento ocurre es muy pequeña, pero el número de intentos es muy grande, entonces el evento actual ocurre algunas veces.
En teoría de probabilidad y estadística, la distribución de Poisson es una distribución de probabilidad discreta. asi tiempo fijo si estos eventos ocurren con una frecuencia media conocida y son independientes del tiempo discurrido desde el último evento.
La función de masa de la distribución de Poisson es:
donde λ es un parámetro positivo que representa la frecuencia esperada del fenómeno modelado por la distribución.
Tanto el valor esperado como la varianza de una variable aleatoria con distribución de Poisson son iguales a λ. Los momentos de orden superior son polinomios de Touchard en λ cuyos coeficientes tienen una interpretación combinatorio. De hecho, cuando el valor esperado de la distribución de Poisson es 1, entonces según la fórmula de Dobinski, el n-ésimo momento iguala al número de particiones de tamañon.
La moda de una variable aleatoria de distribución de Poisson con un λ no entero es igual a la parte entera de lamda, el mayor de los enteros menores que λ . Cuando λ es un entero positivo, las modas son λ y λ − 1.
La función generadora de momentos de la distribución de Poisson con valor esperado λ es
Las variables aleatorias de Poisson tienen la propiedad de ser infinitamente divisibles.
La divergencia Kullback-Leibler desde una variable aleatoria de Poisson de parámetro λ0 a otra de parámetro λ es
Como consecuencia del teorema central del límite, para valores grandes de λ, una variable aleatoria de Poisson X puede aproximarse por otra normal dado que el cociente
converge a una distribución normal de media nula y varianza 1.
Función de distribución(cdf)
Función característica
Ejemplo:
Si en promedio, llegan tres pacientes por minuto al servicio de emergencia del hospital del Niño durante la hora del almuerzo. ¿Cuál es la probabilidad de que en un minuto dado, lleguen exactamente dos pacientes?
Datos: l = 3 pacientes por minuto
Para resolver esto utilizamos al Excel. De las funciones estadísticas, seleccionamos la función POISSON.
Elegimos los parámetros
El resultado es igual a 0.224041808
Ahora lo resolveremos en R
Dando el mismo resultado.
Distribución Normal
La distribución normal fue presentada por vez primera por Abraham de Moivre en un artículo del año 1733,2 que fue reimpreso en la segunda edición de su The Doctrine of Chances, de 1738, en el contexto de cierta aproximación de la distribución binomial para grandes valores de n. Su resultado fue ampliado por Laplace en su libroTeoría analítica de las probabilidades (1812), y en la actualidad se llama Teorema de De Moivre-Laplace.
Gauss, que afirmaba haber usado el método desde 1794, lo justificó rigurosamente en 1809 asumiendo una distribución normal de los errores. El nombre de Gauss se ha asociado a esta distribución porque la usó con profusión cuando analizaba datos astronómicos3 y algunos autores le atribuyen un descubrimiento independiente del de De Moivre.4 Esta atribución del nombre de la distribución a una persona distinta de su primer descubridor es un claro ejemplo de la Ley de Stigler.
Esta distribución es frecuentemente utilizada en las aplicaciones estadísticas. Su propio nombre indica su extendida utilización, justificada por la frecuencia o normalidad con la que ciertos fenómenos tienden a parecerse en su comportamiento a esta distribución.
Muchas variables aleatorias continuas presentan una función de densidad cuya gráfica tiene forma de campana.
En otras ocasiones, al considerar distribuciones binomiales, tipo B(n,p), para un mismo valor de p y valores de n cada vez mayores, se ve que sus polígonos de frecuencias se aproximan a una curva en "forma de campana".
Función de densidad
Se dice que una variable aleatoria continua X sigue una distribución normal de parámetros μ y σ y se denota X~N(μ, σ) si su función de densidad está dada por:
donde μ (mu) es la media y σ (sigma) es la desviación típica (σ2 es la varianza).
Se llama distribución normal "estándar" a aquélla en la que sus parámetros toman los valores μ = 0 y σ = 1. Para esta la función de densidad tiene la siguiente expresión:
La función de distribución de la distribución normal está definida como sigue:
La función generadora de momentos se define como la esperanza de e(tX). Para una distribución normal, la función generadora de momentos es:
como puede comprobarse completando el cuadrado en el exponente.
La función característica se define como la esperanza de eitX, donde i es la unidad imaginaria. De este modo, la función característica se obtiene reemplazando t por it en la función generadora de momentos.
Para una distribución normal, la función característica es:
Aproximación de la Binomial por la Normal (Teorema de De Moivre) :
Demostró que bajo determinadas condiciones (para n grande y tanto p como q no estén próximos a cero) la distribución Binomial B(n, p) se puede aproximar mediante una distribución normal
Ejemplo:
Se supone que los resultados de un examen siguen una distribución normal con media 78 y varianza 36. Se pide:
¿Cuál es la probabilidad de que una persona que se presenta el examen obtenga una calificación superior a 72?
Veremos en la pantalla
El resultado es igual a 0.01092888
Complemento
El Teorema del Límite Central
El Teorema del límite central establece que bajo ciertas condiciones (como pueden ser independientes e idénticamente distribuidas con varianza finita), la suma de un gran número de variables aleatorias se distribuye aproximadamente como una normal.
La importancia práctica del Teorema del límite central es que la función de distribución de la normal puede usarse como aproximación de algunas otras funciones de distribución. Por ejemplo:
Una distribución binomial de parámetros n y p es aproximadamente normal para grandes valores de n, y p no demasiado cercano a 1 ó 0 (algunos libros recomiendan usar esta aproximación sólo si np y n(1 − p) son ambos, al menos, 5; en este caso se debería aplicar una corrección de continuidad).
La normal aproximada tiene parámetros μ = np, σ2 = np(1 − p).
La normal aproximada tiene parámetros μ = np, σ2 = np(1 − p).
Una distribución de Poisson con parámetro λ es aproximadamente normal para grandes valores de λ.
La distribución normal aproximada tiene parámetros μ = σ2 = λ.
La distribución normal aproximada tiene parámetros μ = σ2 = λ.
La exactitud de estas aproximaciones depende del propósito para el que se necesiten y de la tasa de convergencia a la distribución normal. Se da el caso típico de que tales aproximaciones son menos precisas en las colas de la distribución. El Teorema de Berry-Esséen proporciona un límite superior general del error de aproximación de la función de distribución.
Conclusiones
Las distribuciones que en este trabajo se trataron brevemente están relacionadas entre sí cubriendo más aplicaciones a la vida real, en general podemos decir que cada una de estas aporta a campos trascendentales desde hospitales hasta política, ya que la exactitud en los resultados que estas nos ofrecen facilitan la toma de decisiones para grandes instituciones.
Bibliografía
Introduction to the theory of statistics, Alexander Mood















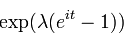












LA INFORMACION ACERCA DE LAS DISTRIBUCIONES ESTA BIEN, CREO QUE LE FALTA RESALTAR UN POCO LOS TITULOS AL BLOG, PONER EJEMPLOS DONDE SE APLIQUEN LAS DISTRIBUCIONES Y EL VIDEO.
ResponderEliminarESPERO Y PUEDAS CHECAR MI BLOG. HASTA LUEGO!!!!
http://leydebildelosgrandesnumerosytcl.blogspot.com